The Prisoners’ Dilemma
The prisoners’ dilemma is a story about two criminals who have been captured by the police. Let’s call them Bonnie and Clyde. The police have enough evidence to convict Bonnie and Clyde of the minor crime of carrying an unregistered gun, so that each would spend a year in jail. The police also suspect that the two criminals have committed a bank robbery together, but they lack hard evidence to convict them of this major crime. The police question Bonnie and Clyde in separate rooms and offer each of them the following deal:
“Right now, we can lock you up for 1 year. If you confess to the bank robbery and implicate your partner, however, we’ll give you immunity and you can go free. Your partner will get 20 years in jail. But if you both confess to the crime, we won’t need your testimony and we can avoid the cost of a trial, so you will each get an intermediate sentence of 8 years.”
If Bonnie and Clyde, heartless bank robbers that they are, care only about their own sentences, what would you expect them to do? Figure 1 shows their choices.
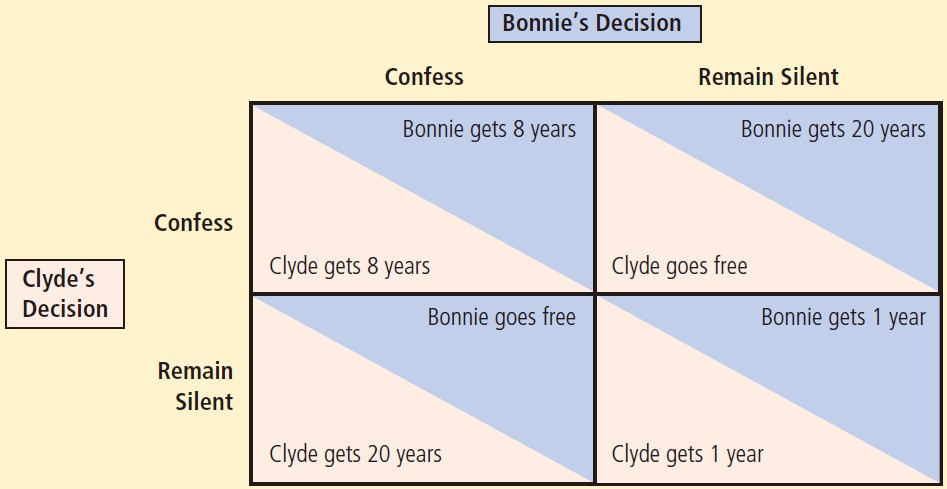 Figure 1 In this game between two criminals suspected of committing a crime, the sentence that each receives depends both on his or her decision whether to confess or remain silent and on the decision made by the other.
Figure 1 In this game between two criminals suspected of committing a crime, the sentence that each receives depends both on his or her decision whether to confess or remain silent and on the decision made by the other.
Each prisoner has two strategies: confess or remain silent. The sentence each prisoner gets depends on the strategy he or she chooses and the strategy chosen by his or her partner in crime.
Consider first Bonnie’s decision. She reasons as follows: “I don’t know what Clyde is going to do. If he remains silent, my best strategy is to confess, since then I’ll go free rather than spending a year in jail. If he confesses, my best strategy is still to confess, since then I’ll spend 8 years in jail rather than 20. So, regardless of what Clyde does, I am better off confessing.”
In the language of game theory, a strategy is called a dominant strategy if it is the best strategy for a player to follow regardless of the strategies pursued by other players. In this case, confessing is a dominant strategy for Bonnie. She spends less time in jail if she confesses, regardless of whether Clyde confesses or remains silent.
Now consider Clyde’s decision. He faces the same choices as Bonnie, and he reasons in much the same way. Regardless of what Bonnie does, Clyde can reduce his jail time by confessing. In other words, confessing is also a dominant strategy for Clyde.
In the end, both Bonnie and Clyde confess, and both spend 8 years in jail. This outcome is a Nash equilibrium: Each criminal is choosing the best strategy available, given the strategy the other is following. Yet, from their standpoint, the outcome is terrible. If they had both remained silent, both of them would have been better off, spending only 1 year in jail on the gun charge. Because each pursues his or her own interests, the two prisoners together reach an outcome that is worse for each of them.
You might have thought that Bonnie and Clyde would have foreseen this situation and planned ahead. But even with advanced planning, they would still run into problems. Imagine that, before the police captured Bonnie and Clyde, the two criminals had made a pact not to confess. Clearly, this agreement would make them both better off if they both lived up to it, because they would each spend only 1 year in jail. But would the two criminals in fact remain silent, simply because they had agreed to? Once they are being questioned separately, the logic of self-interest takes over and leads them to confess. Cooperation between the two prisoners is difficult to maintain, because cooperation is individually irrational.
FYI: The Prisoners’ Dilemma Tournament
Imagine that you are playing a game of prisoners’ dilemma with a person being “questioned” in a separate room. Moreover, imagine that you are going to play not once but many times. Your score at the end of the game is the total number of years in jail. You would like to make this score as small as possible. What strategy would you play? Would you begin by confessing or remaining silent? How would the other player’s actions affect your subsequent decisions about confessing?
Repeated prisoners’ dilemma is a complicated game. To encourage cooperation, players must penalize each other for not cooperating. Yet the strategy described earlier for Jack and Jill’s water cartel—defect forever as soon as the other player defects—is not very forgiving. In a game repeated many times, a strategy that allows players to return to the cooperative outcome after a period of noncooperation may be preferable.
To see what strategies work best, political scientist Robert Axelrod held a tournament. People entered by sending computer programs designed to play repeated prisoners’ dilemma. Each program then played the game against all the other programs.
The “winner” was the program that received the fewest total years in jail. The winner turned out to be a simple strategy called tit-for-tat. According to tit-for-tat, a player should start by cooperating and then do whatever the other player did last time. Thus, a tit-for-tat player cooperates until the other player defects; then she defects until the other player cooperates again. In other words, this strategy starts out friendly, penalizes unfriendly players, and forgives them if warranted. To Axelrod’s surprise, this simple strategy did better than all the more complicated strategies that people had sent in.
The tit-for-tat strategy has a long history. It is essentially the biblical strategy of “an eye for an eye, a tooth for a tooth.” The prisoners’ dilemma tournament suggests that this may be a good rule of thumb for playing some of the games of life.
Reference
Principles of Economics