The Condorcet Voting Paradox
Most advanced societies rely on democratic principles to set government policy. When a city is deciding between two locations to build a new park, for example, we have a simple way to choose: The majority gets its way. Yet for most policy issues, the number of possible outcomes far exceeds two. A new park could be placed in many possible locations. In this case, as the 18th-century French political theorist Marquis de Condorcet famously noted, democracy might run into some problems trying to choose the best outcome.
For example, suppose there are three possible outcomes, labeled A, B, and C, and there are three voter types with the preferences shown in Table 1. The mayor of our town wants to aggregate these individual preferences into preferences for society as a whole. How should he do it?
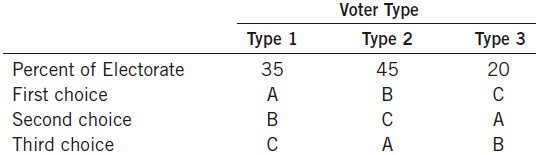
Table 1 If voters have these preferences over outcomes A, B, and C, then in pairwise majority voting, A beats B, B beats C, and C beats A.
At first, he might try some pairwise votes. If he asks voters to choose first between B and C, voter types 1 and 2 will vote for B, giving B the majority. If he then asks voters to choose between A and B, voter types 1 and 3 will vote for A, giving A the majority. Observing that A beats B, and B beats C, the mayor might conclude that A is the voters’ clear choice.
But wait: Suppose the mayor then asks voters to choose between A and C. In this case, voter types 2 and 3 vote for C, giving C the majority. That is, under pairwise majority voting, A beats B, B beats C, and C beats A. Normally, we expect preferences to exhibit a property called transitivity: If A is preferred to B, and B is preferred to C, then we would expect A to be preferred to C. The Condorcet Paradox is that democratic outcomes do not always obey this property. Pairwise voting might produce transitive preferences for society in some cases, but as our example in the table shows, it cannot be counted on to do so.
One implication of the Condorcet paradox is that the order in which things are voted on can affect the result. If the mayor suggests choosing first between A and B and then comparing the winner to C, the town ends up choosing C. But if the voters choose first between B and C and then compare the winner to A, the town ends up with A. And if the voters choose first between A and C and then compare the winner to B, the town ends up with B.
The Condorcet paradox teaches two lessons. The narrow lesson is that when there are more than two options, setting the agenda (that is, deciding the order in which items are voted on) can have a powerful influence over the outcome of a democratic election. The broad lesson is that majority voting by itself does not tell us what outcome a society really wants.
FYI: Arrow’s Impossibility Theorem
Since political theorists first noticed Condorcet’s paradox, they have spent much energy studying existing voting systems and proposing new ones. For example, as an alternative to pairwise majority voting, the mayor of our town could ask each voter to rank the possible outcomes. For each voter, we could give 1 point for last place, 2 points for second to last, 3 points for third to last, and so on. The outcome that receives the most total points wins. With the preferences in Table 1, outcome B is the winner. (You can do the arithmetic yourself.) This voting method is called a Borda count for the 18th-century French mathematician and political theorist who devised it. It is often used in polls that rank sports teams.
Is there a perfect voting system? Economist Kenneth Arrow took up this question in his 1951 book Social Choice and Individual Values. Arrow started by defining what a perfect voting system would be. He assumes that individuals in society have preferences over the various possible outcomes: A, B, C, and so on. He then assumes that society wants a voting system to choose among these outcomes that satisfies several properties:
- Unanimity: If everyone prefers A to B, then A should beat B.
- Transitivity: If A beats B, and B beats C, then A should beat C.
- Independence of irrelevant alternatives: The ranking between any two outcomes A and B should not depend on whether some third outcome C is also available.
- No dictators: There is no person who always gets his way, regardless of everyone else’s preferences.
These all seem like desirable properties of a voting system. Yet Arrow proved, mathematically and incontrovertibly, that no voting system can satisfy all these properties. This amazing result is called Arrow’s impossibility theorem.
The mathematics needed to prove Arrow’s theorem is beyond the scope of this book, but we can get some sense of why the theorem is true from a couple of examples. We have already seen the problem with the method of majority rule. The Condorcet paradox shows that majority rule fails to produce a ranking of outcomes that always satisfies transitivity.
As another example, the Borda count fails to satisfy the independence of irrelevant alternatives. Recall that, using the preferences in Table 1, outcome B wins with a Borda count. But suppose that suddenly C disappears as an alternative. If the Borda count method is applied only to outcomes A and B, then A wins. (Once again, you can do the arithmetic on your own.) Thus, eliminating alternative C changes the ranking between A and B. This change occurs because the result of the Borda count depends on the number of points that A and B receive, and the number of points depends on whether the irrelevant alternative, C, is also available.
Arrow’s impossibility theorem is a deep and disturbing result. It doesn’t say that we should abandon democracy as a form of government. But it does say that no matter what voting system society adopts for aggregating the preferences of its members, it will in some way be flawed as a mechanism for social choice.
Reference
Principles of Economics